平均・分散・標準偏差・正規分布・標準正規分布まとめ
データを扱うとき、ただ数値を並べるだけでは比較が難しいため「加工」して見やすくします。
平均は誰でも知っている指標ですが、分散・標準偏差・正規分布・標準正規分布は「なぜ必要なのか」その意味をかみ砕きまくって、理解を深めていきましょう。
1. 平均（Mean）
データの「基準点」として使う。これは一般的に使われるヤツ。
平均 = （すべての値の合計） ÷ （データの個数）
$$\text{平均} = \frac{\sum x_i}{n}$$
例： データ 60, 70, 80
60＋70＋80 ÷ 3 ＝ 平均 70
2. 偏差と分散
偏差（Deviation）： 各データが平均からどれだけズレているか
- 式：偏差 = データの値 − 平均
$$\text{偏差} = x_i – \bar{x}$$ - 例：データ 60, 70, 80 が 平均 70 からのズレなので → 偏差：−10, 0, +10
分散（Variance）： 偏差を二乗して平均したもの（ばらつきの大きさ）
- 式：分散 = （偏差²の合計） ÷ （データの個数）
$$\text{分散}(\sigma^2) = \frac{\sum (x_i – \bar{x})^2}{n}$$ - 例：偏差² = 100, 0, 100 → 分散 = (100+0+100)/3 ≈ 66.7
なぜ二乗するのか？
偏差は正負があるので、そのまま平均すると必ず0になります。二乗すれば「大きさ」だけが残り、ズレの大きい値を強調できます。ただし単位が二乗されてしまう（点数², cm²など）ので、必要に応じて平方根をとって元の単位に戻します（＝標準偏差）。
3. 標準偏差と偏差値
標準偏差（σ）： 分散の平方根。単位を元に戻した「直感的なばらつき」。
$$\text{標準偏差}(\sigma) = \sqrt{\sigma^2}$$
- 正規分布なら「平均 ±1σ」に約68%が含まれる
- 「1σ上にいる」＝「上位16%付近にいる」
偏差値：平均との差を標準化した指標
- 式：偏差値 = 50 + 10 × (得点 − 平均) ÷ 標準偏差
$$\text{偏差値} = 50 + 10 \times \frac{x – \mu}{\sigma}$$ - 流れ： (得点 − 平均) → ÷ 標準偏差 → ×10 → +50
- 目安：50＝平均、60=上位16%付近、70=上位2.5%付近、40=下位16%付近
4. 正規分布（Normal Distribution）
特徴： 平均を中心に左右対称の「釣鐘型」分布。平均 μ が中心、標準偏差 σ が広がりを決める。
→つまり平均と中央値と最頻値が一致します。
身長、体重、テストの点数、製品の誤差など、たくさんの小さな要因の積み重ねで決まる量は自然に正規分布に近づきます。
経験則（68-95-99.7ルール）：
- 平均 ±1σ → 約68%
- 平均 ±2σ → 約95%
- 平均 ±3σ → 約99.7%
5. 標準正規分布（Standard Normal Distribution）
特徴： 平均 μ = 0、標準偏差 σ = 1 の正規分布。統計の基準となる分布。
Zスコア（標準化）： $$Z = \frac{x – \mu}{\sigma}$$
- 「データが平均から何σ離れているか」を表す
- 異なる分布のデータを共通の物差しで比較できる
- 確率表（Z表）で範囲確率を求められる
- 外れ値判定や機械学習の前処理にも使われる
6. 正規分布と標準正規分布の違い
- 正規分布： 実際のデータの分布。平均や標準偏差はデータごとに異なる → 現実の形
- 標準正規分布： どんな正規分布も「平均0・標準偏差1」に変換した基準形 → 共通の物差し
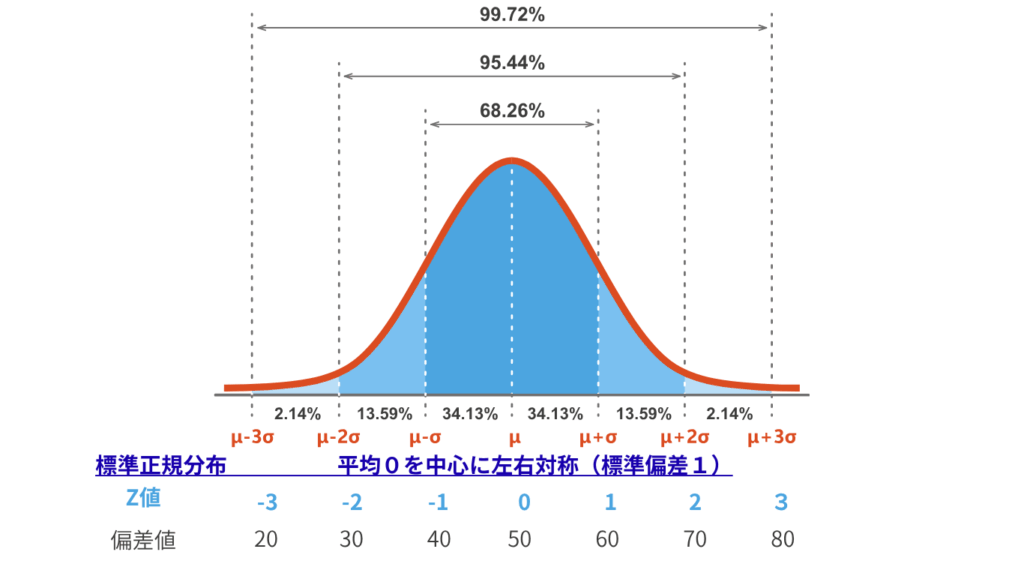
※ この図は正規分布の釣鐘型と、±1σ〜±3σの範囲を示しています。
Zスコアの数直線上で、偏差値60は+1σ、偏差値70は+2σに相当します。
7. まとめ
- 平均 = データの基準点
- 偏差 = 平均からのズレ
- 分散 = 偏差²の平均（ばらつきの大きさ）
- 標準偏差 = 分散の平方根（単位を戻した直感的なばらつき）
- 「1σ」= 平均からのひとまとまりの距離（上位16%の目安）
- 偏差値 = Zスコアを「平均50・標準偏差10」に換算した指標
- 正規分布 = 世の中の多くのデータが従う釣鐘型分布
- 標準正規分布 = 平均0・標準偏差1に変換した基準分布
- 違い = 正規分布は「現実の形」、標準正規分布は「共通の物差し」
📘 シリーズ記事の流れ
次の記事 ▶️：
📚 シリーズトップ：
コメント