機械学習ではモデルの「正しさ具合」を定量的に評価できます。 用語自体は難しくないのですが、似た表現が多く混乱しがちです。 DS検定の問題を問いていると、問題文が少し違うだけでどっちがどっちだったかと悩むことも多くいです。分類と回帰では評価の仕方が異なるため、整理しておきましょう。
2. 分類モデルの評価指標
2-1. 混同行列(Confusion Matrix)
分類モデルの性能を語るときの出発点は「混同行列」です。 実際の正解と予測結果を照らし合わせると、次の4パターンに分かれます。
| 実際\予測 | 陽性(Positive) | 陰性(Negative) |
|---|---|---|
| 実際に陽性 | TP(True Positive) =正しく陽性 | FN(False Negative) =陽性を見逃し |
| 実際に陰性 | FP(False Positive) =誤って陽性 | TN(True Negative) =正しく陰性 |
意味は英語で読んだ方が早いですね。
この4つの組み合わせが、すべての評価指標の基盤になります。
2-2. Accuracy(正解率)
全体のうち正しく当てた割合)です。 ※Accuracy の あ は当たり
$$\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$
Accuracy = (TP + TN) / (TP + TN + FP + FN)
当たり / 全部
直感的でわかりやすいですが、クラス不均衡(例:不良品が1%しかないデータ)では 「全部良品と予測しても99%正解」となり、実用性が低いこともあります。
2-3. Precision(適合率)
「陽性と予測した中で、本当に陽性だった割合」です。 ※Precision のPは ピンポイント
$$\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}$$
Precision = TP / (TP + FP)
本当に陽性(正解) /(陽性と予想した全部=本当に陽性+実際は陰性)
適合という言葉は「モデルが陽性と予測したうち、どれだけ的(テキ)確に当てたか」と覚えておきましょう。 誤報を減らしたいときに重視されます。
例:医療診断で「がんではない人を誤ってがんと判定する」ことを避けたい場合。
★どうしても覚えられずごっちゃになる人(私)は、てきごう と よそう 末尾 う が同じ
2-4. Recall(再現率)
「実際の陽性をどれだけ拾えたか」です。 ※リ・コールは 呼び・戻し で再現をイメージ
$$\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}$$
Recall = TP / (TP + FN)
本当に陽性(正解)/(実際に陽性だった全部=本当に陽性⁺間違えたけど実際は陽性)
再現という言葉は「実際の陽性をきちんと再現できているか」という意味で覚えておきましょう。 見逃しを避けたいときに重視されます。
例:スパム検出で「スパムを見逃す」ことを避けたい場合。
★どうしても覚えられずごっちゃになる人(私)は、さいげん じっさい の さいが同じ
2-5. F1スコア
PrecisionとRecallのバランスを取る指標です。
$$F1 = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$$
2×(適合率×再現率)/(適合率+再現率)
この式、私的にはモヤモヤします(率を足すとか割るとかイミフ)ですが、調和平均をとるということはそういうことだそうです。足すことも割ることも(どちらも正なら)数字を大きくすることですが、このような式を使うことで2つの値のバランスをとれるらしいです。
どちらか一方に偏らず、総合的に評価したいときに使われます。
2-6. PrecisionとRecallのトレードオフ
分類モデルは「閾値(カットオフ)」を変えることでPrecisionとRecallのバランスが変わります。
誤検出しても見逃したくないのか、見逃しても誤検出は避けたいのか ということですね。
- 閾値を厳しくすると → Precisionは上がるがRecallは下がる
- 閾値を緩くすると → Recallは上がるがPrecisionは下がる
この関係を可視化するのがROC曲線やPR曲線です。 詳しくは別記事 → ROC曲線とAUC
3. 回帰モデルの評価指標
分類とは異なり、回帰モデルは「数値のズレ」を評価します。
3-1. MAE :Mean Absolute Error(平均絶対誤差)
これは普通に、予測値と実測値の差の絶対値を平均したものです。
$$\text{MAE} = \frac{1}{n}\sum_{i=1}^{n} |y_i – \hat{y}_i|$$
MAE = Σ|y – ŷ| / n
全てのデータの合計 / データの個数 = 平均をとっている
直感的で「平均的にどれくらい外れているか」がわかります。
例:住宅価格予測で「平均して20万円の誤差」。
3-2. RMSE :Root Mean Squared Error (二乗平均平方根誤差)
誤差を二乗して平均し、平方根を取ったものです。
$$\text{RMSE} = \sqrt{\frac{1}{n}\sum_{i=1}^{n} (y_i – \hat{y}_i)^2}$$
2乗を戻すのにルートする 2乗して合計 / データの個数 =2乗の平均
誤差はプラスとマイナスがありますが単純に足すと誤差要素が消えるので2乗しているということです。
例 プロットが右肩上がりで誤差があると下記のような図になります
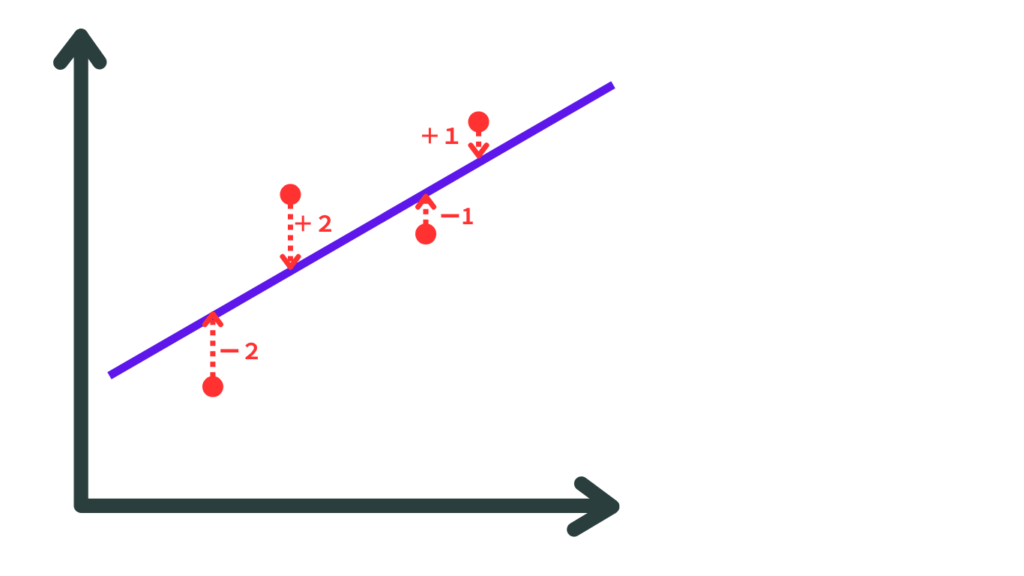
誤差はマイナスだったりプラスだったりするので、全部足すと
(ー2) + 2 +(-1) +1 =0 を4で割るって平均はゼロ
となっちゃうので(これは間違い)
(ー2)² + 2² +(-1)²+1² =10 を4で割って2乗平均は2.5
これだと実際の誤差の2乗となる大きさになるのでルートをとって1.58
また、 2乗するので大きな誤差をより強くペナルティとして評価できます。
例:外れ値があるとRMSEは大きく跳ね上がります。
3-3. R²(決定係数)
0〜1の範囲で「モデルがどれだけデータを説明できているか」を示します。
$$R^2 = 1 – \frac{\sum (y_i – \hat{y}_i)^2}{\sum (y_i – \bar{y})^2}$$
1-(実際の値と予測値の差の2乗の合計)/(実際の値と平均値の差の2乗の合計)
→実際の平均と予想値の差を割合にして1から引くので1~0になるってことですね。
例:R² = 0.85 → データの85%を説明できている。
3-4. MAEとRMSEの違い
- MAE: 平均的なズレをフラットに評価。外れ値に強い。
- RMSE: 大きなズレを強調。外れ値に敏感。
実務では両方を併用して「平均的な誤差」と「大きな外れの影響」を確認します。
4. 分類と回帰の比較表
| モデル種類 | 主な指標 | 特徴 | 典型的な用途 |
|---|---|---|---|
| 分類 | Accuracy | 全体の正解率 | バランスの取れたデータ |
| 分類 | Precision | 陽性予測の純度 | 医療診断、不正検知 |
| 分類 | Recall | 陽性の拾い漏れ率 | スパム検出、不良品検知 |
| 分類 | F1 | PrecisionとRecallのバランス | 総合評価 |
| 回帰 | MAE | 平均的なズレ | 直感的な誤差評価 |
| 回帰 | RMSE | 大きな誤差を強調 | 外れ値を重視する予測 |
| 回帰 | R² | 説明力の割合 | モデルの当てはまり度合い |
5. まとめ
- 分類モデルは「正しく当てるか/見逃さないか」を評価する。
- 回帰モデルは「どれだけズレているか/どれだけ説明できているか」を評価する。
- ROC曲線とAUCは別記事で詳解 → ROC曲線とAUC
📘 シリーズ記事の流れ
次の記事 ▶️:

📚 シリーズトップ:




コメント