【DS検定対策1】ベクトル計算をやさしく理解する（和・内積・ノルム・距離）

データサイエンスを学び始めると、まず最初に出てくるのがベクトルです。
高校物理で「スカラーはただの数」「ベクトルは方向がある」と意味不明の授業を受け、
「なんじゃそれ？」と思ったまま、「一生使うことは無いな」と思いましたが、まさかここで出てくるとは。。。

データサイエンスやAIでは、このベクトルが「特徴を方向として扱う」として使われます。このように使い道を学んでいたら、高校物理も楽しかったのでしょうね！

たとえば感情性をy軸、話題性をx軸にして、その大きさを長さとすると、単語をベクトル化できるのです。そんなこと、よく思いついたものです。ベクトルを使うことで向きの近さや大きさにより、単語同士の関連度を判断するというのが自然言語処理の仕組みです。人間の会話でも「話題の方向性」といいますが、その言葉の通りですね。点と点の位置関係や距離感をベクトルで扱うことで、デジタル技術（コンピューター）が数値の計算で処理を実現することができるようになります。

ということで、ベクトルアレルギーを取り除いて、基礎知識を一緒に身につけていきましょう。

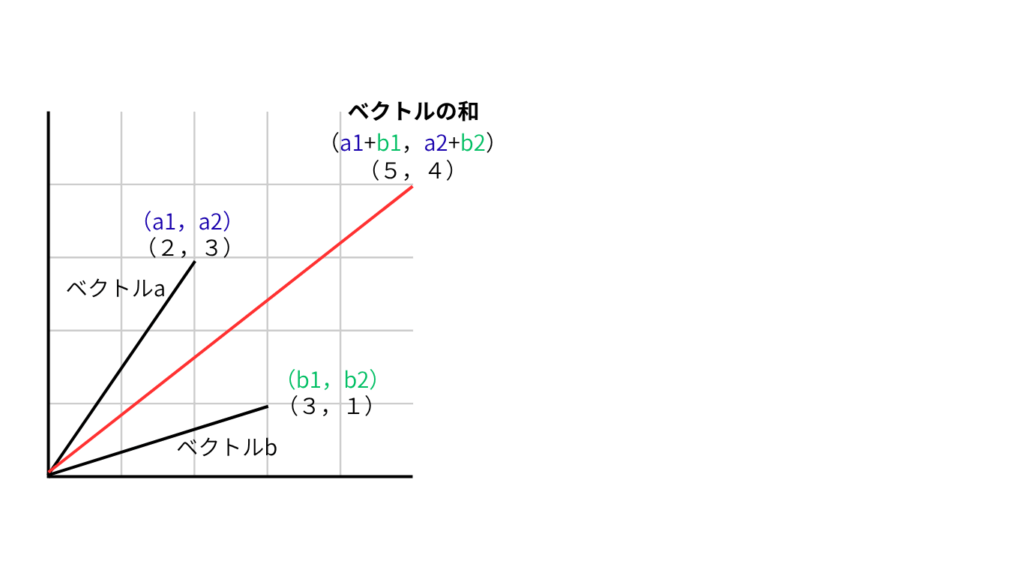
ベクトルの和（Vector Addition）

複数の方向（力・移動・速度など）を「合成」して一つの結果を得る。
２つの情報を足し合わせることで、特徴の平均やクラスタの中心を求めたり、単語や意味の合成、勾配の合成（学習方向）、次元を圧縮し主成分を作る　などに使われます。

計算方法：
成分ごとに足すだけ。
ベクトルa = \(\vec{a} = (a_1, a_2)\)
ベクトルb = \(\vec{b} = (b_1, b_2)\)
ベクトルの合計 a + b =　\(\vec{a} + \vec{b} = (a_1+b_1, a_2+b_2)\)

ベクトルの内積（Dot Product）

二つのベクトルが「どれだけ同じ方向を向いているか」を測る、または、一方を他方の方向に「写し取る（射影）」というのが内積です。
端的に言えばベクトルをスカラーにしている（つまり掛けて足して、ベクトルをただの数値にしている）ってことになります。

計算方法：
成分ごとに掛けて足す：
$$\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2$$

と言葉で言ってもピンとこないと思うので下記の図を見てください。ベクトルが同じ方向を向いていれば写し取る量が大きくなるので、情報が似ているということを、数字の大きさで表せる（ことで比較したり理解して処理ができるようになる）ということです。

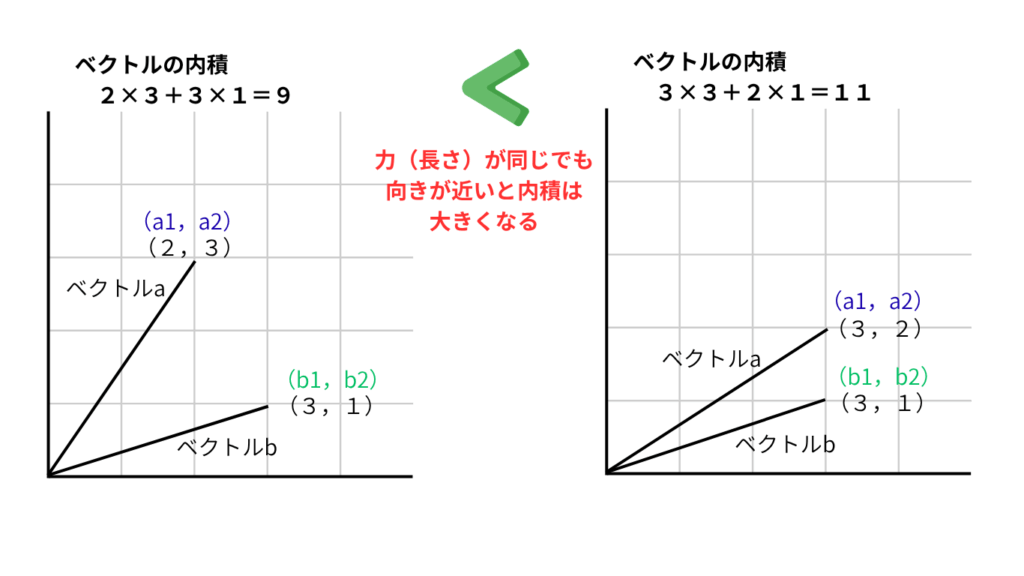
掛け算なので、どちらか一方がマイナスだと逆方向と言えますし、どちらもマイナスだとかけてプラスになるので大きさとして大きくなるということです。

ユークリッドノルム（L2ノルム）

ノルムとは「規範」「標準」という意味を持ちますが、数学では「ベクトルの大きさ（長さ）」をあらわす関数です。DS検定の勉強をしていると色々と言い方が変わるので混乱しますが、ざっくりノルムとは距離であると覚えてしまいましょう。

目的：
ベクトルそのものの「大きさ（長さ）」を測る。つまり2点間の「最短距離」。

計算方法：
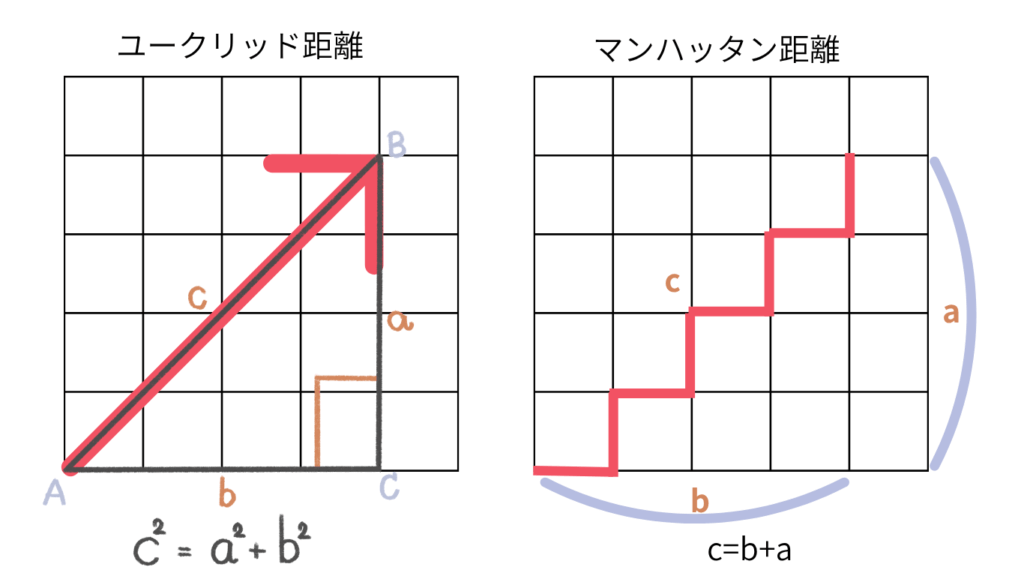
ピタゴラスの定理、覚えていますか？直角三角形は底辺と高さを2乗して足すと斜辺の2乗になるので、√で2乗を戻せば斜線の長さが求まるアレです。
$$||\vec{a}|| = \sqrt{a_1^2 + a_2^2}$$ ・例：(0,0)から(4,4)まで $$\sqrt{4^2 + 4^2} = \sqrt{32} \approx 5.656$$

結果でわかること：
・ベクトルの「長さ」＝ユークリッド距離
・ピタゴラスの定理は「直角三角形の斜辺を求める」＝「最短距離を求める」こと

マンハッタン距離（L1ノルム）：
　L2ノルムに対してL1ノルムというのもあります。縦横の格子に沿って「ジグザグに進む距離」
です。
$$||\vec{a}||_1 = |a_1| + |a_2|$$ ・例：(0,0)から(4,4)まで = 4+4 = 8

イメージ：
・ユークリッド(L2) = 正確な距離　　「空を飛ぶカラスのような最短ルート」
　　　誤差の二乗を使うため、大きな誤差に強くペナルティを与える → 滑らかに調整される
　　　機械学習では、滑らかな誤差を重視するモデルに使用　（リッジ回帰、SVM）

・マンハッタン（L1） = ざっくりの距離　「道路に沿って曲がりながら進むルート」
　　　誤差の絶対値 → 一部の重みをゼロにしやすい（スパース性）
　　　機械学習では、不必要な情報の重みをゼロにして、データを軽くして効率を上げる時に使用
　　（Lasso回帰）

まとめ

和 = 複数の作用を合成する → 成分を足す → 合成結果がわかる

内積 = 方向の一致度や射影を測る → 成分を掛けて足す → ベクトルをスカラーにする

ノルム = ベクトルの大きさ＝最短距離を測る → ピタゴラスの定理で導かれる

ユークリッド距離 = 直線距離（最短ルート）

マンハッタン距離 = 格子をジグザグに進む距離（縦横の合計）

DS検定対策では、計算練習などがでてきますが、ベクトルって何に使われるのか？という本質を理解しておきましょう。実際にどのようにベクトルが使われるのかを知った方が面白いです。
「ベクトルとか数式ばかりで難しい」から、移動や力のイメージに置き換え「情報も持つ意味を方向と捉え、その強さを長さとして扱う」という理解です。

知識の定着は、覚えるよりも「なるほど、そういう意味か」と納得してつけていきましょう。