【DS検定対策2】固有値・固有ベクトルとは？行列変換で“向きが変わらないベクトル”を図解でやさしく解説

固有値・固有ベクトルって？
─方向そのまま、長さだけ変わる。情報の伸びしろを知る

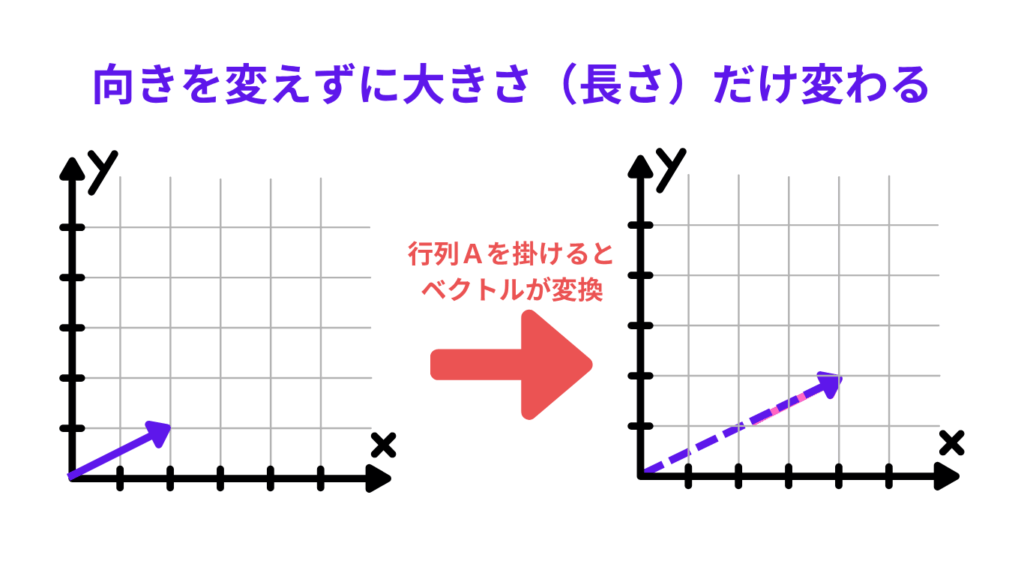
「固有値」「固有ベクトル」は、ざっくり言うと、行列を掛け算しても“向きが変わらない”ベクトルがあって、そのときの倍率（長さの変化）が「固有値」です。といってもなんのこっちゃですよね。
この「向きが変わらない」ってところがミソで、簡単にいえばベクトルの長さだけの伸び縮みする話です。ほとんどのベクトルは行列をかけると向きも長さも変わるんですが、特定のベクトルだけは向きがそのまま長さを変えられるというものです。

そんなことして何がうれしいの？って話ですが、AI、データサイエンスの正解ではベクトルは情報を数値化し強さは特徴（方向）を表しています。固有ベクトルを求めることで、その情報が持つポテンシャル（伸びしろ）を特定し、学習に生かしているのです。

ベクトルの再確認

まずはベクトルって何？というところから再確認します。
ベクトルは「向き」と「長さ」を持った矢印のようなものです。

ベクトルの長さを変えるースカラー倍と行列変換の違い

• スカラー倍：ただの数字（スカラー）をかけるだけ → 向きはそのままで、長さだけ変わる
  例：右向きの矢印が2倍の長さになるだけ
• 行列変換：変換ルール（行列）をかける → ほとんどのベクトルは、向きも長さも変わる
  例：右向きの矢印が斜め上に曲がって、長さも変わる

固有ベクトルってどういうもの？

行列 A に対して、あるベクトルx だけは：

$$A\vec{x} = \lambda\vec{x}$$

という式が成り立つことがあります。このとき：

• x は「固有ベクトル」
• λ（ラムダ）は「固有値」＝倍率（スカラー）

この式の意味は、「行列 A をかけても、ベクトル x の向きは変わらず、長さだけ λ 倍になる」ということ。（スカラーで長さを変えるだけではなく、ベクトルでも同じことができるということ）
つまり、行列変換でも長さを変えられ“向きが変わらない”という特別なベクトルがあるんです。
それが「固有ベクトル」です。そして、そのときの倍率が「固有値」です。

ここで大事なのは、主語が「ベクトル」じゃなくて「行列」だということ。
「行列 A は、向きを変えずに長さだけ変えるベクトル x を持っている」という見方が本質です。

λI ってなんで出てくるの？

上の式 $$A\vec{x} = \lambda\vec{x}$$を、左辺にまとめると

$$A\vec{x} – \lambda\vec{x} = 0$$

となるのですが、A は「行列」、λ は「ただの数字（スカラー）」なので、直接引き算できません。

そこで λ を「行列っぽく」するために、単位行列 I を使います。

$$I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$

単位行列 I は、行列界の「1」みたいなもので、掛け算しても形が変わらない便利なやつです。

$$A\vec{x} – (\lambda I)\vec{x} = 0$$

と書き換えることで、両方とも「行列 × ベクトル」の形になって、引き算ができるようになります。x で括ると：

$$(A – \lambda I)\vec{x} = 0$$

この式が「固有ベクトルの条件式」です。

固有値の求め方

この式は、x がゼロ（つまりゼロベクトル）のときは、どんな λ でも成り立ってしまいます。
なぜなら、ゼロに何をかけてもゼロになるからです。

でも、知りたいのは「ゼロじゃないベクトル x に対して、向きはそのままで長さだけ変わるような λ があるか？」ということ。
つまり、ゼロベクトルは除外して、「x ≠ 0 のときに式が成り立つ条件」を探す必要があります。
ということで　(A − λI) 　の方がゼロになればいいんじゃん　という話になります。

そこで使うのが「行列式（determinant）」という道具です。
行列式は、行列の“変形力”みたいなものを表す数値で、ゼロになると「変形できない方向がある」ことを意味します。

式はこうなります：

$$\det(A – \lambda I) = 0$$

この式には x（ベクトル）が含まれていないので、λ（スカラー）だけの世界になります。
これが「固有方程式」と呼ばれるものです。

具体例で見てみよう

行列A
$$A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}$$
の場合：

まず λI を作ります。　
$$I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$
なので
$$\lambda I = \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix}$$

それを A − λI にすると：
$$\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} – \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix} = \begin{bmatrix} 2-\lambda & 1 \\ 1 & 2-\lambda \end{bmatrix}$$


この行列の行列式(ad-bc)を求めます：
$$\det\begin{bmatrix} 2-\lambda & 1 \\ 1 & 2-\lambda \end{bmatrix} = (2-\lambda)(2-\lambda) – 1 \times 1$$ $$= (2-\lambda)^2 – 1$$ $$= \lambda^2 – 4\lambda + 3$$

この式を因数分解します：

$$\lambda^2 – 4\lambda + 3 = (\lambda – 1)(\lambda – 3)$$

ここで「この式がゼロになる条件」を考えます。
掛け算の結果がゼロになるには、どちらかの項がゼロになればOKなので：

• $$\lambda – 1 = 0 \quad \Rightarrow \quad \lambda = 1$$
• $$\lambda – 3 = 0 \quad \Rightarrow \quad \lambda = 3$$

つつまり、この行列 A には
　λ = 1 のとき向きが変わらないベクトル
　λ = 3 のとき向きが変わらないベクトル
がそれぞれ存在するということになります。

DS検定では固有ベクトルまでの求め方は問われないので、計算の詳細はここでは省略しますが、（実際には「(A−λI)x=0」という式を解くことで出てきます）
λ=1 のときは (1,−1) の方向、λ=3 のときは (1,1) の方向が固有ベクトルとなります。

つまり、データサイエンスでは情報をベクトルとして扱うので、情報の意味（方向）を変えることなく、その強さや大きさを 1倍（維持）、3倍（協調）にする行列が存在する、という理解につながります。

まとめ

「固有値・固有ベクトルは、複雑な変形を“方向ごとの伸び縮み”に分解する道具です。行列が“どの方向にどれだけ効くか”を定量化することで、データの本質を見抜けます。 データサイエンスでは、これを使って“伸びしろの方向（固有ベクトル）”と“その大きさ（固有値）”を特定し、ノイズを減らし、安定性を判断し、重要構造を抽出します。

＜具体例＞

• PCA（次元削減）: ノイズを減らし本質だけ残す 　
  固有ベクトル＝データの“情報が一番多い方向”、固有値＝その“情報量の大きさ”
• 安定性の直感: 固有値が 1 より小さい方向は繰り返し作用で縮む→安定化、
  1 より大きい方向は伸びる→不安定
• ネットワーク（PageRank 型）: “リンクが集まる方向”を固有ベクトルで捉える＝重要ノードの抽出