【DS検定対策3】順列・組合せ・条件付き確率・ベイズの定理を初心者向けにやさしく図解で解説

　順序、組み合わせ、条件付確率　難しい話ではないのですが、どっちがどっち？となる混乱分野ですね。どっちだっけ？　とならぬように、本来の意味で考えてましょう。

---

順列（Permutation）＝ 並べ方（順番あり）

順列とは「選んだものを順番をつけて並べる」場合の数。順序をつけるというのは、　ABC　と　ACB　と　CBA　を区別するということなので、通り数としては大きくなる（計算要素が少ない方）ということです。

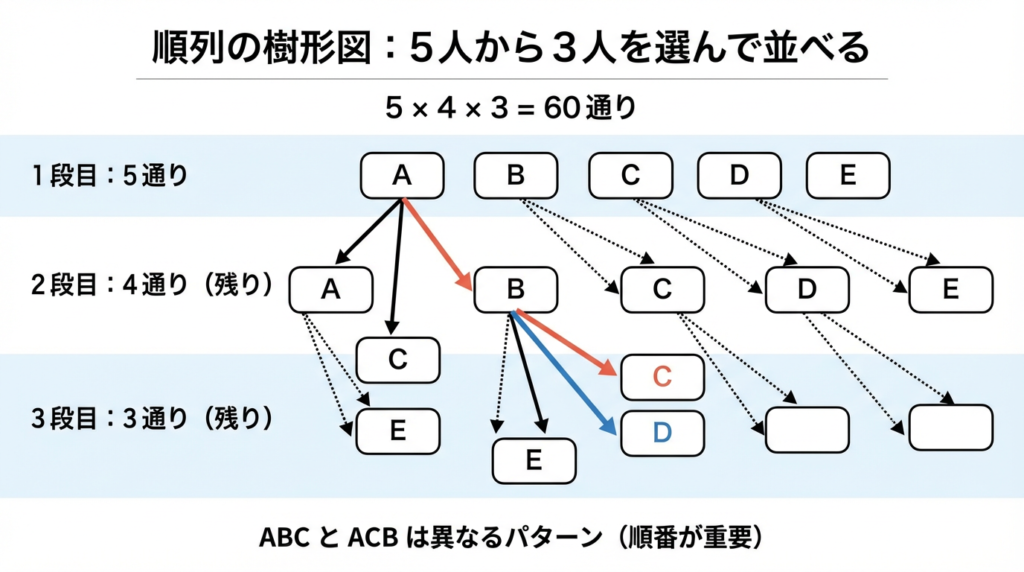
例： 5人の中から3人を選んで並べる（正副　とか　班長、書記　とか） → 何通り？

1. 1人目は 5 通り
2. 2人目は 残り4 通り
3. 3人目は 残り3 通り

→ 5 × 4 × 3 = 60 通り

計算式
順列の数 = （総数）! ÷ （総数 − 選びたい数）!
総数の組み合わせから、選ばなかった人の並びを数えすぎているので、その分を割って調整しています。
※「!」は階乗を示す記号で、その数から1まで掛けるという意味。例：3! = 3×2×1

例題： 5人の中から3人を選んで並べる場合

5! ÷ (5−3)! = (5×4×3×2×1) ÷ (2×1) = 5×4×3　＝60通り

※全部かけてから割るのではなく、同じ数字を通分すると早いです。
　 5×4×3×2×1 
ーーーーーーーーー　＝　5×4×3　＝60　
　　　　2×1

---

組み合わせ（Combination）＝ 選び方（順番なし）

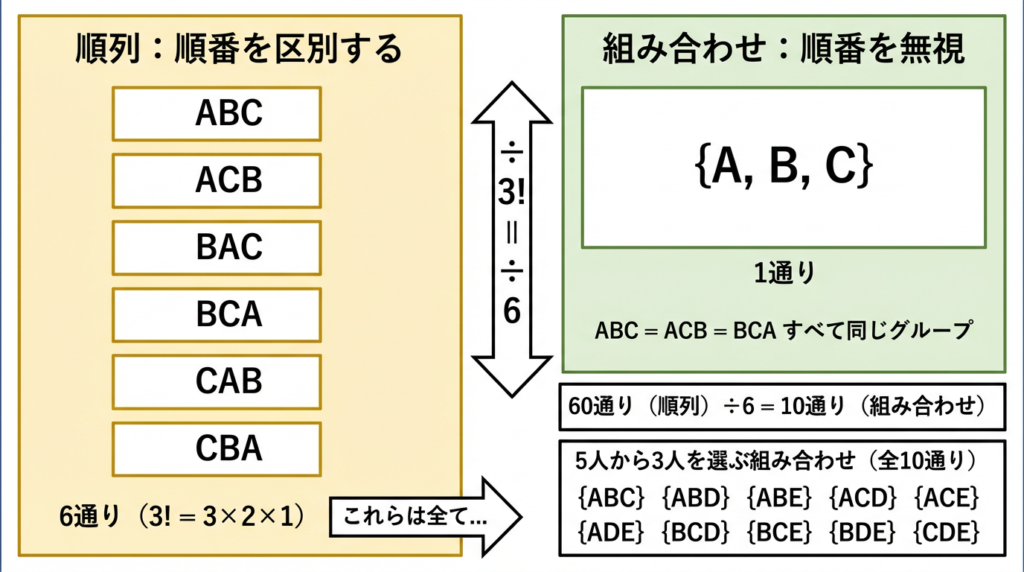
組み合わせとは「選ぶだけで順番を気にしない」場合の数。順列との違いは、順番を気にしないのでABC　と　ACB　と　CBAでも区別しないということ。なので、順列を区別しなくていい”選びたい数の分（階乗）”でさらに割ることになります。

例： 5人の中から3人を選ぶ → 何通り？

計算は順列とまずは同じ60通りですが、この中には「ABC」「CAB」「BCA」のように、順序を気にしなければ同じ通りになるものが含まれています。そこで順列をさらに（選びたい数）! を割ればOKです。

計算式
組み合わせの数 = 順列 ÷ （選びたい数）!

例題： 5人の中から3人を選ぶ場合

(5! ÷ (5−3)!) ÷ 3!　= (5×4×3×2×1) ÷ (2×1×3×2×1)　= 5×2 = 10通り

※全部かけてから割るのではなく、同じ数字を通分すると早いです。
　 5×2(4)　×3×2×1
ーーーーーーーーー　＝　5×2　＝10　
　2×1　×3×2×1
　

---

条件付き確率（Conditional Probability）

条件付き確率とは「ある条件Ｂが起きた世界で、加えて別の事象Ａが発生する確率」を表します。

式と意味
$$P(A \mid B) = \frac{P(A \cap B)}{P(B)}$$

• B = 「ある条件」 → すでに起きていること、前提となる出来事
• A = 「別の事象」 → その条件のもとで調べたい出来事
• P(B) = 条件Bが起きる確率
• P(A ∩ B) = AとBが同時に起きる確率
• P(A | B) = 「Bが起きた世界」に限定したときのAの確率

例題：
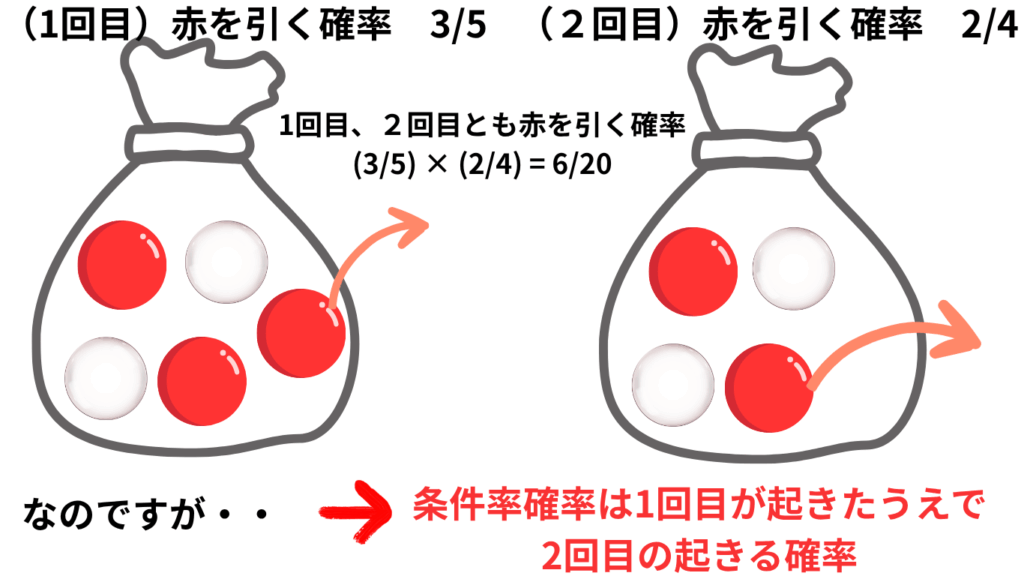
袋に赤玉3個、白玉2個が入っている。1個取り出したら赤だった。次に取り出す玉が赤である確率は？

• 条件B = 「1回目に赤を引いた」
• 事象A = 「2回目に赤を引く」　⇒　この時、条件Ａの後なので赤を2つ引いている

全体：5個 → 赤3、白2
条件Bが起きた後の状況：残りは赤2、白2

条件付き確率：「ある条件が起きたときに、別の事象が起きる確率」
P(A | B) =　P（別の事象）　　　　　　　÷　P（ある条件）
　　　　＝　P(2回目が赤 ∩ 1回目が赤) ÷ P(1回目が赤)

分子 = 1回目赤かつ2回目赤 = (3/5) × (2/4) = 6/20
分母 = 1回目赤 = 3/5

結果：P(A | B) = (6/20) ÷ (3/5) = 1/2

順列・組み合わせとのつながり

• 確率は「場合の数 ÷ 全体の数」で計算する
• その「場合の数」を数えるのに順列や組み合わせを使う
• 条件付き確率は「全体」を「条件が起きた世界」に限定して考える

---

ベイズの定理

条件付き確率は「ある条件が起きた　ときに、別の事象が起きる確率」でした。
ベイズの定理はその逆で、「ある結果が出たときに、原因が何だったかを　推測する確率」です。
例えば、ある選手が1試合に3本のホームラン＋10奪三振出したという結果がでたら、それは大谷翔平だろう　と推測するみたいな話です。
医療やマーケティングなどで広く使われている定理になります。

式と意味

$$P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}$$

• P(A)：原因Aが起きる確率（事前確率）
• P(B | A)：原因Aのときに結果Bが起きる確率（条件付き確率）
• P(B)：結果Bが起きる全体の確率（周辺確率）
• P(A | B)：結果Bが起きたときに、原因Aだった確率（事後確率）

例題：検査と病気

ある病気の人は全体の1%（100人中1人）。 　⇒病気にかかる確率は低い
この病気を調べる検査は、以下のような性能です：

• 病気の人が陽性になる確率（感度）：90%　⇒一見検出率が高そう？
• 健康な人が陽性になる確率（偽陽性率）：5%　⇒偽陽性もある・・

検査が陽性だったとき、本当に病気である確率は？　　

ステップで考える：

1. 病気の人（1人）が陽性になる確率：　　 0.01×0.9=0.009
2. 健康な人（99人）が陽性になる確率： 　 0.99×0.05=0.0495
3. 陽性になる全体の確率： 　　　　　　　 0.009+0.0495=0.0585
4. 陽性だった人が本当に病気である確率： 0.009÷0.0585≒0.154

つまり、検査が陽性でも病気の確率は約15.4%。　「陽性＝病気」とは限らないとなります。

---

まとめ

• 順列 は　全体数から選ぶ数分を引いた数の階乗
• 組み合わせ は　順列を　順番を区別しない数分　割る
• 条件付き確率は「条件が起きた世界」に限定して確率を考える
• 結果から原因を推測するベイズの定理

---