帰無仮説・対立仮説・第一種の過誤・第二種の過誤
仮説検定は帰無仮説と対立仮説がイメージと逆で混乱しがちです。どっちが立証したい仮説なのか?を明確になるように整理していきましょう。
私は開発現場出身ですがバグの原因究明でも「原因仮説を立てて検証する」という考え方はよく使いました。私の経験では「バグの原因となりうる要因を洗い出して発生メカニズムの仮説をたて立証する」ことが多かったですが、統計学では「否定したい仮説(帰無仮説)を棄却できるか」を調べるという逆の発想になります。この考え方は応用範囲が広く、面白いです。
帰無仮説
「帰無」とは「無に帰す」=「特別な効果はないとみなす」という意味。
つまり「差がない」「効果がない」「変化がない」という立場を仮定します。
例:
- 薬の効果を調べる → 「薬に効果はない」
- コインが公平か調べる(いかさま を見抜きたい) → 「表と裏の確率は同じ」
→ 検定はまず「何も起きていない」という基準点である帰無仮説から始めます。
対立仮説
「対立」とは「帰無仮説に対立する立場」。
帰無が「無(効果なし)」なら、対立は「有(効果あり)」です。
例:
- 薬の効果を調べたい → 「薬に効果がある」
- コインが偏っているか調べたい → 「表と裏の確率が違う」
→ 対立仮説は「本当に検証したい仮説」。
「対立」という言葉に惑わされがちですが、実際には“本命仮説”です。
(注意!) before/after には3つの状態があります
①よくなる(大きくなる、増える)
②変わらない(効果がない)
③悪くなる(小さくなる、減る)
とっても当たり前のことを言ってますが、非常に重要です。
「良くなる」が対立仮説ならなら、帰無仮説は 「良くならない」:片側検定
「変わる」が対立仮説なら、帰無仮説は 「変わらない」 :両側検定
と微妙(というか全然)違います。問題でひっかからないように注意しましょう。
第一種の過誤
定義は「本当は帰無仮説が正しいのに、それを棄却してしまう誤り」です。
- 帰無仮説は「効果なし」
- 本当は効果がないのに「効果あり」と結論づけてしまう
- = 存在しない効果をあると信じてしまう
これは最悪の結果です。なぜなら「効かない薬を効くと信じて世に出す」ということになるからです。実害や不具合を生む可能性が高く、必ず避けなければならない誤りです。
しかし、帰無仮説が正しいということは、本命仮説を却下することになるので、検証する人にとって好ましくない結果になりがちです。ここに心情的には何が何でも却下したい! などという邪な考えが入り込まないように、しっかりと検証し却下すべきものは却下しないとですね。
なのでこの確率を「有意水準 α(%)」として厳しく制御します。(効果なしの確率が、わずかでもあれば帰無仮説を採用する勇気)
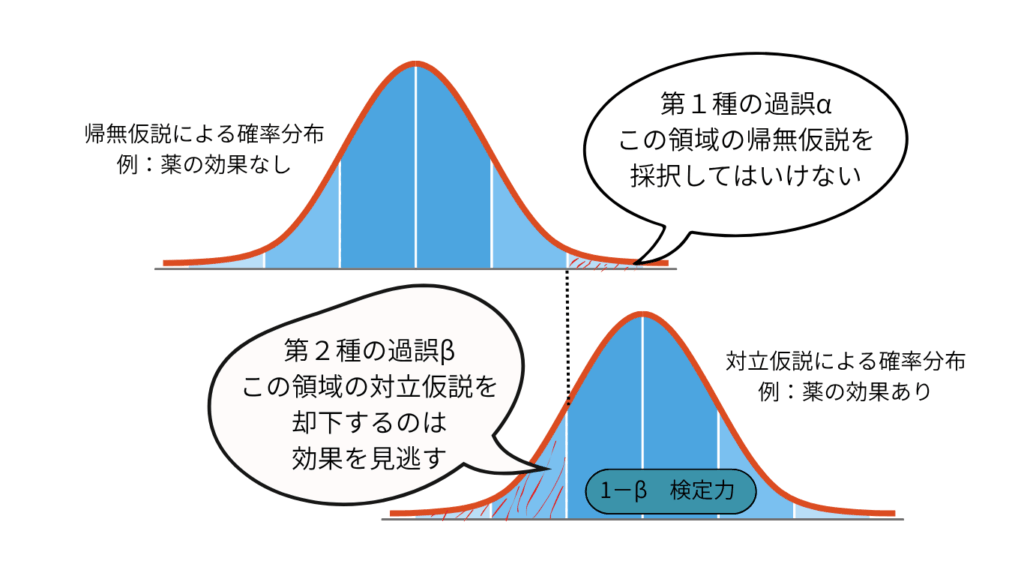
帰無仮説の確率分布の右端(裾)に観測値が位置した場合、その観測値よりさらに極端な領域の面積(図の斜線部)を p値 といいます。 この p値は「もし本当に効果がないとしたら、今回のような結果が偶然に出る確率」を表しています。 そして、この p値があらかじめ決めた基準である 有意水準 α(%) より小さい場合、帰無仮説を棄却します(図の吹き出しの意味)。
第二種の過誤
定義は「本当は帰無仮説が間違っているのに、それを棄却できない誤り」です。
- 帰無仮説は「効果なし」
- 実際には効果があるのに「効果なし」と結論づけてしまう
- = 存在する効果を見逃す
これは「もったいない」誤りです。効く薬を「効かない」と判断して捨ててしまうことになるからです。実害は出ませんが、科学的な進歩を遅らせ、ビジネス的な損失を生み出します。
この確率は β と表され、1 − β は「検出力(Power)」=効果を見抜く力です。
過誤の整理
逆説的な表現なので混乱しがちです。表で整理すると理解しやすくなります。
| 項目 | 帰無仮説(H0) | 対立仮説(H1) |
|---|---|---|
| 定義 | 効果や差は「ない」と仮定する | 効果や差は「ある」と仮定する |
| 役割 | 検定の出発点(まずは疑わない立場) | 検定で証明したい主張 |
| 例:薬の効果 | 「新薬は従来薬と効果に差がない」 | 「新薬は従来薬より効果がある」 |
| 例:硬貨 | 「この硬貨は公平(表と裏は50%)」 | 「この硬貨は偏っている」 |
| 検定結果 | 棄却されなければ維持される | 棄却されれば採択される |
| 覚え方 | 「帰無=帰って無い(差は無い)」 | 「対立=対抗して差がある」 |
第一種・第二種の過誤
| 真実 | 検定で棄却 | 検定で棄却しない |
|---|---|---|
| 帰無仮説が正しい | 第一種の過誤(誤って棄却) | 正しい判断 |
| 帰無仮説が誤り | 正しい判断 | 第二種の過誤(見逃し) |
→ 第一種の過誤は「ないものをあると誤認」=実害が出るので最悪。
→ 第二種の過誤は「あるものをないと見逃す」=安全側だが進歩を逃す。
有意水準と検出力の関係
第一種の過誤を減らす(αを小さくする)と、第二種の過誤は増えやすくなります。
つまり「安全を優先すると見逃しやすくなる」というトレードオフがあります。
検定の流れ
- 帰無仮説と対立仮説を立てる
- データを集める
- 統計量を計算する
- 有意水準と比較して、帰無仮説を棄却するか判断する
検定手法
平均値を比較する検定
| 検定名 | データの関係性 | 分散の仮定 | 主な用途 | 見分けのポイント |
|---|---|---|---|---|
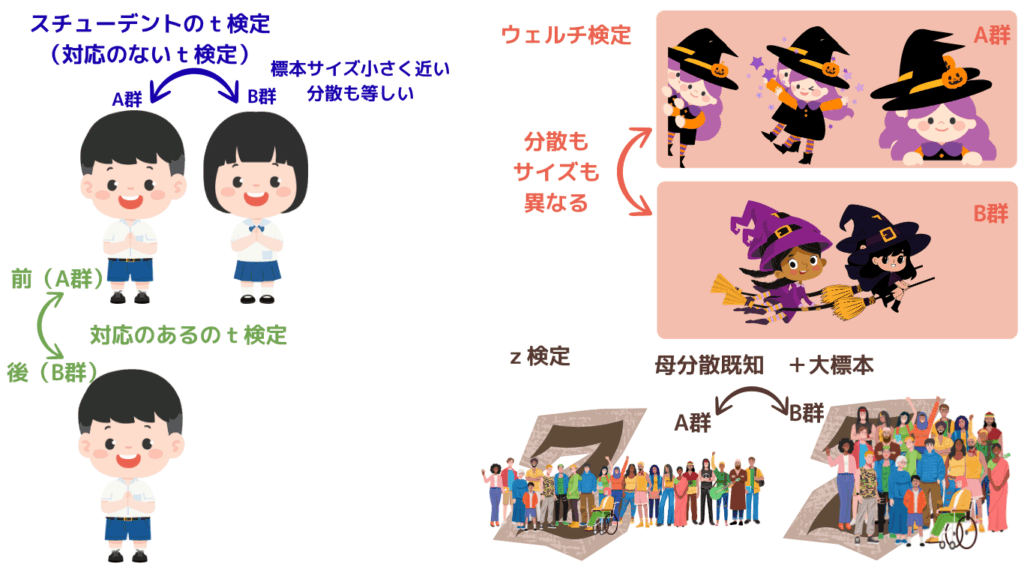
| スチューデントのt検定 (対応のないt検定) | 別々の2群 (独立) | 分散が等しい | 2群の平均比較(例:A群 vs B群) | 標本(サンプル)サイズが近く、分散が等しい前提 |
| ウェルチ検定 | 別々の2群 (独立) | 分散が異なる | 2群の平均比較(分散・サイズが異なる場合) | 分散が異なる or 標本サイズが不均等 |
| 対応のあるt検定 | 同一対象の 前後比較 | 差の分布が正規 | 同一被験者の施策前後などの比較 | 同じ人・同じ対象の変化を比較する場合 |
| z検定 (平均の差) | 別々の2群 (独立) | 母分散が既知 | 母分散が既知かつ標本サイズが大きい場合 | 母分散が既知+大標本が条件(実務では稀) |
分布・カテゴリの違いを比較する検定
| 検定名 | 用途 | 備考(DS検定観点) |
|---|---|---|
| カイ二乗検定 | カテゴリ間の分布差・独立性 | 平均値の比較ではない。クロス集計表で使用。 |
分散の違いを比較する検定
| 検定名 | 用途 | 備考(DS検定観点) |
|---|---|---|
| F検定 | 分散の差 | ばらつきの比較。分散分析(ANOVA)にも関連。 |
まとめ
- 帰無仮説 = 「無に帰す」=効果なし・差なし
- 対立仮説 = 「帰無に対立する」=効果あり・差あり
- 第一種の過誤 = 存在しない効果をあると誤認 → 実害を生むので最悪
- 第二種の過誤 = 存在する効果を見逃す → 実害はないが進歩を逃す
- 有意水準 α = 第一種の過誤を起こす確率 → 厳しく制御する
- 検出力(1−β) = 効果を見抜く力 → 第二種の過誤を減らす指標
- 検定の目的 = データから帰無仮説を棄却できるかどうかを判断すること
- 分散が等しい時はスチューデントのt検定、分散が異なる場合はウェルチ検定
📘 シリーズ記事の流れ
次の記事 ▶️:

📚 シリーズトップ:




コメント