【DS検定対策6】集合と論理記号を形で理解｜ベン図・AND・OR・NOTをやさしく整理

　ベン図といわれてもピンとこないかもしれませんが、円を2つ書いて同じものが重なる部分になる、「仲間分け」または「グループ分け」の図で見たことはあるでしょう。論理記号がわかる人にはリンクさせると印象に残るかもしれません。ここはそんなに難しくはないので、直感で思い出せるようにしていきたいと思います。

1. 和集合（Union）

記号： A ∪ B

意味：
「A または B に属するもの全部」。両方に含まれているものも、まとめて入ります。

形のイメージ：
∪ は「カップを広げた形」。両方の集合をすくい取って、ひとつにまとめる感じです。

---

2. 積集合（Intersection）

記号： A ∩ B

意味：
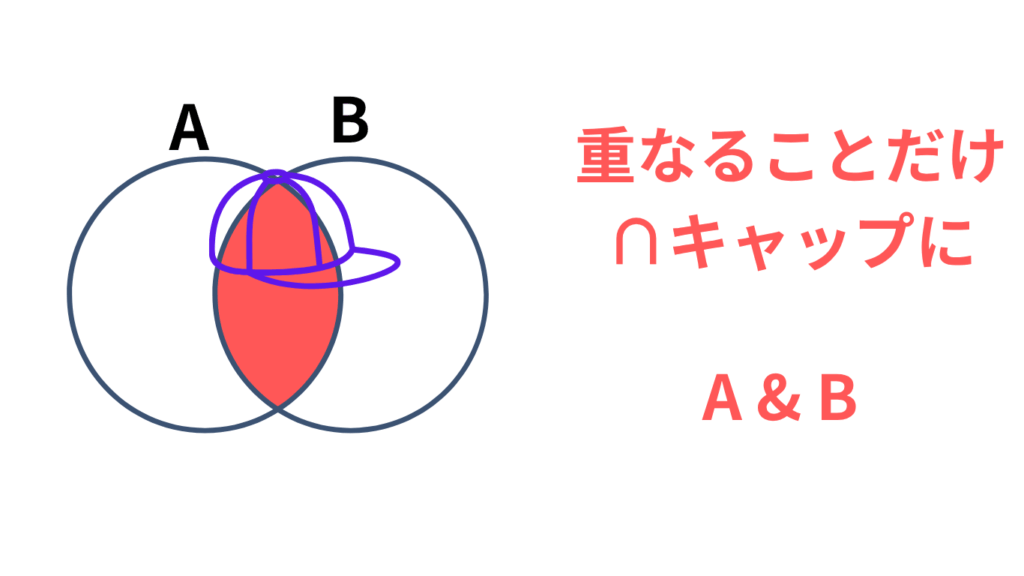
「A かつ B に属するもの」。両方に同時に含まれている部分だけ。

形のイメージ：
∩ は「帽子の形」。重なる部分だけ帽子をかぶせるイメージです。（実際に業界ではキャップっていうらしいです）

---

3. 差集合（Difference）

記号： A − B

意味：
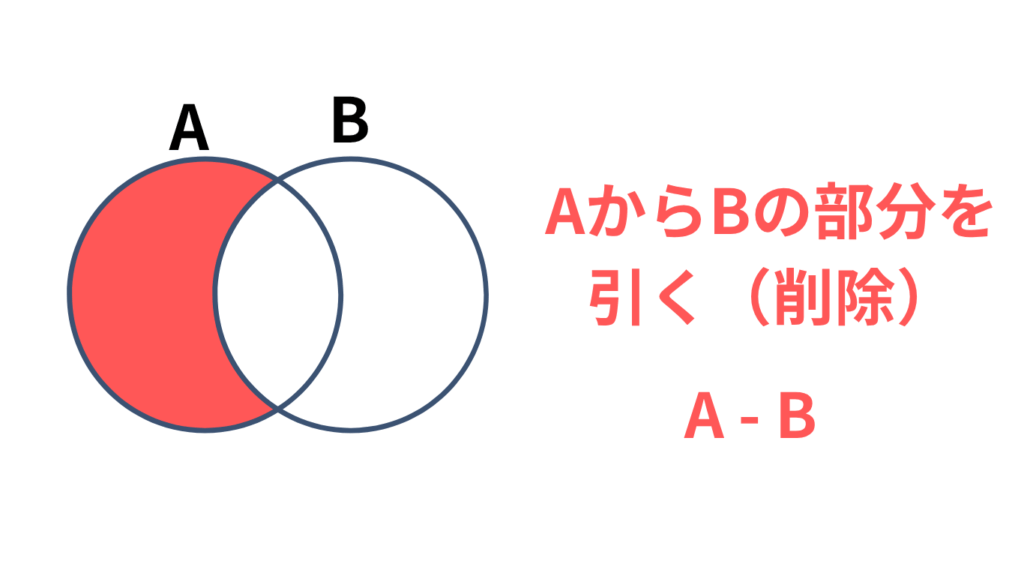
「A に属するけど、B には属さないもの」。B の部分を A から削り取った残りです。

形のイメージ：
「−」は引き算の記号そのもの。A から B を引き去るイメージです。

---

4. 補集合（Complement）

記号： A′ または A^c

意味：
「全体集合 U の中で、A に含まれないもの全部」。つまり、A の外側にある全ての部分です。

形のイメージ：
・′（ダッシュ）は「外に追いやった印」
・c は complement（補う）の頭文字
→ A の外側を塗るようなイメージです。

---

5. 論理記号と集合のつながり

集合の記号って、実は論理の記号とすごく似ています。DS検定でもよく出てくるので、ここで一緒に見ておきましょう。

• A ∪ B（和集合） → A OR B（A または B）
  　→「どちらかに入っていればOK」ってこと。
  　　　ORはどちらかなので、「AかBのどちらかがTrue（真）ならTrue」っていうことです。
• A ∩ B（共通部分） → A AND B（A かつ B）
  　→「両方に入っていないとダメ」。
  　　AND「AもBも両方がTrue（真）でないとTrueにならない」っていう動きです。
  　　足し算みたいな感じで、両方そろって初めて成立です。
• A′（補集合） → NOT A（A ではない）
  　→「Aに入ってないもの全部」。
  　　NOTは「”じゃない”　なので、逆にする」っていうことで、TrueならFalse、
  　　FalseならTrueになります。

6. まとめ（形と意味で覚える）

• ∪ = カップを広げて「全部まとめる」 → OR
• ∩ =　帽子（キャップ）の形で「重なるところだけ　かぶせる」 → AND
• − = 引き算で「削り取る」
• ′ = 外に追いやる「残りもの」 → NOT
• 論理記号（AND・OR・NOT）は集合記号とつながっている

集合も論理も、形からイメージして覚えてしまいましょう。

（おまけ）データテーブル結合を「集合の形」で一瞬で見抜くコツ

DS検定ではデータテーブルが２つと結合後のテーブルが表示され、結合の種類を問う問題がでます。ベン図は頭にあっても、データテーブルになるとわからなくなる場合もあるので、結果テーブルの特徴でイメージしてみましょう。

結合の種類	集合での形	結果テーブルの特徴
INNER JOIN	A ∩ B	共通するキーだけ残る
LEFT JOIN	A（Bが無い部分は空欄）	A の行がすべて残る
RIGHT JOIN	B（Aが無い部分は空欄）	B の行がすべて残る
FULL OUTER JOIN	A ∪ B	両方の行がすべて残る

ポイントは 「どの行が残っているか」だけを見る こと。 左右が明示されていない問題は、基本的に INNER JOIN（共通部分） を問う形式です。 左右が指定されている場合のみ、LEFT / RIGHT の判定が可能になります。 集合のベン図と対応づけると、テーブル結合の判定は驚くほどシンプルになります。

---