「紙おむつを買う男は、ビールも一緒に買う傾向が非常に高い」
これはデータ分析の本質に迫る有名な逸話だそうです。一見なんの関係もない商品同士ですが、データ分析からこの相関関係が発見されたっていう物語ですね。
この背景を深掘りすると、「週末に紙おむつを買いに頼まれた父親は、自分のビールも一緒に買う」というパターンが多いということが浮かび上がり、この分析に基づいて小売店が紙おむつの近くにビールを陳列したところ、両方の商品の売り上げが大幅に上がったそうです!(事実かどうかは?ですけど) これぞデータ分析の力(の事例)ですね。
この話に例えられているのが、アソシエーション分析と呼ばれる「もしAが起きたら、そのときBも起きる」という If-Then 形式 のルールで、そこで使われる3つの指標が今回のテーマです。
1.アソシエーション分析とは
アソシエーション分析は、膨大な取引データの中から「一緒に発生する項目の組み合わせ(パターン)」を見つける手法です。
例えば、スーパーのレシートには「Aさんはパンと牛乳を購入」「Bさんはパンとバターを購入」など多くの記録(データ)があります。
これらをまとめて分析し、「パンとバターはよく一緒に買われる」といった関係(ルール)を抽出します。
このときルールを「A ⇒ B(Aが起きたらBも起きる)」という形で表し、そのルールの強さや信頼性を測るために使うのが「支持度」「信頼度」「リフト値」ということです。
2.支持度(Support)とは
支持度とは、「全体の中で、AとBが一緒に起きた割合」です。
式で表すと
支持度(A⇒B)= A∩Bの件数 ÷ 全体の件数
例えば1000件の購買データのうち、「おむつとビールを一緒に買った」ケースが80件なら、支持度は8%となります。
「支持」という言葉には「多くの人に支持されている=よく現れる」というニュアンスがあり、「AとBという組み合わせがデータ全体の中でどのくらい“支持”されているか」を示すわけです。
支持度が低いルールは、偶然の可能性が高いため分析対象から除外できるし、逆に、一定以上の支持度をもつルールが“注目に値するパターン”となるわけです。
3.期待信頼度=P(B) ※用語揺れがあるらしいがリフト値の分母
で使用するので ここでは これで
期待信頼度とは、「AとBが独立して起きるなら、どのくらいの確率でBが起きるか」を示す理論的な基準値です。
式: 期待信頼度(A⇒B) = 支持度(B)
例)全体の中でビールを買う人が40%なら、期待信頼度=40%。
つまり、「紙おむつを買ったかどうかに関係なく、偶然でもビールは40%の確率で買われるはず」という普通に期待される基準です。
実際の信頼度がこの期待信頼度より高ければ、「紙おむつを買うとビールも買う」という関係は偶然ではないといえます。
逆に、信頼度が期待信頼度と同じなら、それは単なる偶然の関係にすぎません。
4.信頼度(Confidence)とは
信頼度は、「Aが起きたとき、どのくらいの確率でBも起きるか」を示します。
式で表すと
信頼度(A⇒B)= AかつBの件数 ÷ Aの件数
紙おむつ(A)を買った人が100人、そのうちビール(B)も買った人が80人なら、信頼度は80%です。
ここでの「信頼」とは、「AをきっかけにBを予測しても信頼できるか?」という意味です。
紙おむつ(A)を見たときにビール(B)を“信じてよい”確率、というイメージです。
信頼度が高いルールは「Aが起きたらBもほぼ起きる」という強い関係を示すことになりますね。
ただし、AやBがそもそも人気商品なら、信頼度だけでは本当の関連性を見誤ることもあるので要注意です。(なので、次のリフト値と合わせて判断が必要)
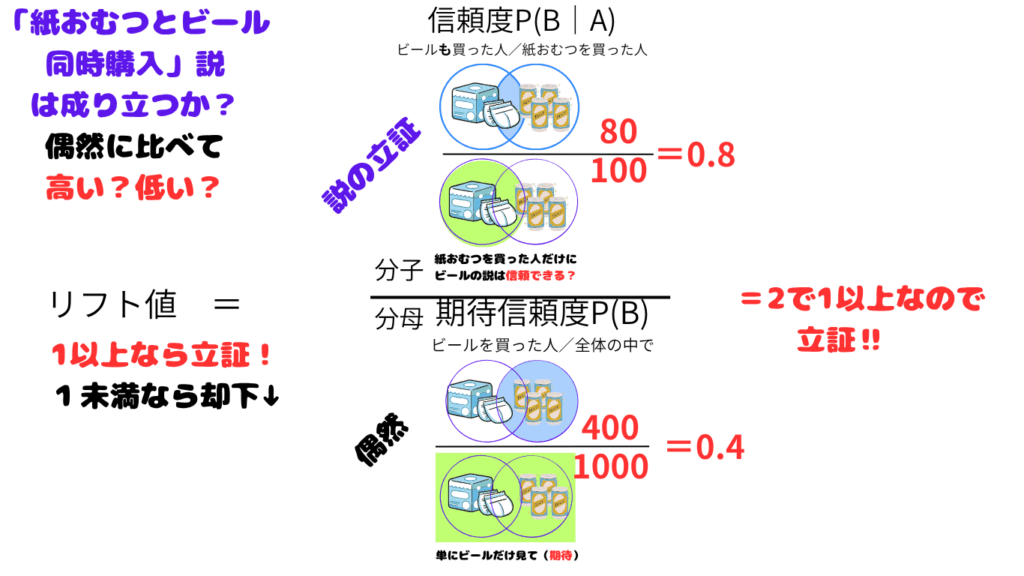
5.リフト値(Lift)とは
最後の指標がリフト値です。
これは「AとBが一緒に起きる頻度が、偶然に比べてどれくらい高いか」を示します。
式で表すと
リフト値(A⇒B)= 信頼度(A⇒B) ÷ Bの出現確率
おむつを買う人が100人中80人がビールも買い、全体の中でビールを買う人が40%だとすると、リフト値は 0.8 ÷ 0.4 = 2.0となります。
数値としては1より上か下かというのが判断基準となっていて、
1より小さい場合は「Aが起きてもBはむしろ起きにくい」となります。(負の相関)
逆に、 リフト値 > 1 なら、AがあるとBが起きやすく、「AがBを押し上げる(liftする)」関係にあるといえます。(正の相関)
つまり、リフト値の「リフト」とは「持ち上げる」「引き上げる」の意味で、「AがあることでBの発生をどれだけ押し上げているか」というイメージです。
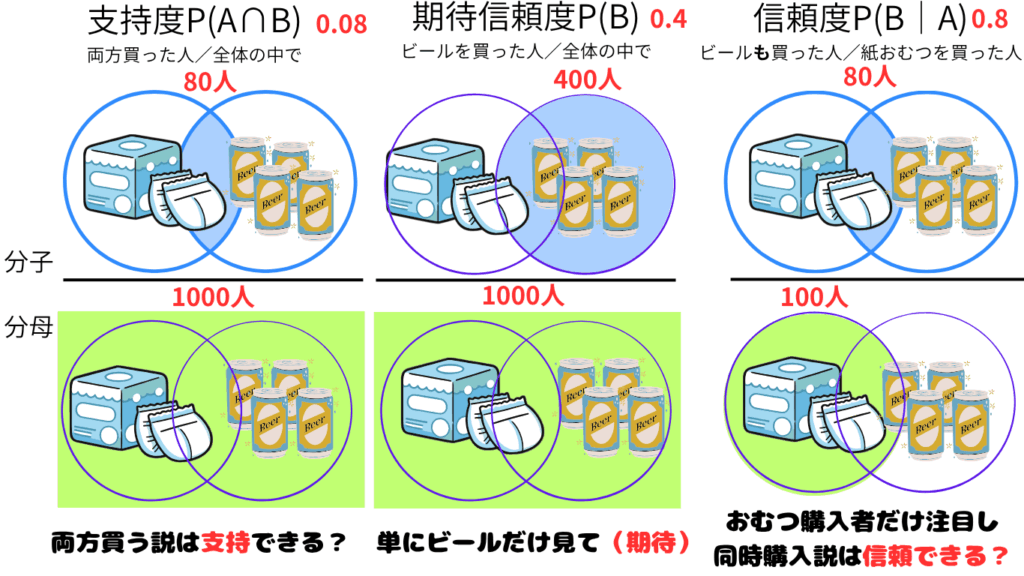
6.4つの指標の関係を図で整理
全体の購入データ件数:N=1000件
おむつ購入者数:A=100人 ビール購入者数:B=400人 両方購入した人:A∩B=80人
7.まとめ
アソシエーション分析は、マーケティングだけでなく、医療・金融・Web行動分析など幅広い分野で使われるそうです。
支持度・信頼度・リフト値の3つを組み合わせて判断することで、「データの中に潜むパターン」を正しく見極めることができるのです。
支持度が高い=十分な事例数があること、信頼度が高い=説(ルール)の確からしさがあること、リフト値が高い=偶然ではない関係があること(説の立証)。この3つをセットで理解しておく感じですね。
(おまけ) ちなみに、どっちから見たリフト値??
問題ではAから見てBのリフト値は?と出題されたりするようですが、AとBはどっちがどっちとなりますよね?今回の記事で逆から見てみましょう。
1. おむつ ⇒ ビール の場合
- 信頼度(おむつを買った人のうちビールも買った割合) 80 ÷ 100 = 0.8
- 期待信頼度(全体でのビール購入率) 400 ÷ 1000 = 0.4
- リフト値 0.8 ÷ 0.4 = 2.0
2. ビール ⇒ おむつ の場合
- 信頼度(ビールを買った人のうちおむつも買った割合) 80 ÷ 400 = 0.2
- 期待信頼度(全体でのおむつ購入率) 100 ÷ 1000 = 0.1
- リフト値 0.2 ÷ 0.1 = 2.0
ということで、リフト値は「Aから見てもBから見ても同じ値」になります。
これは、どちらから見ても 分子は共通の「同時購入数」80 であり、分母の組み合わせ(100と400、1000と1000)が入れ替わるだけなので、最終的に同じ形になります。
(80 ÷ 100)/(400 ÷ 1000)=(80×1000)/(100×400)
(80 ÷ 400)/(100 ÷ 1000)=(80×1000)/(400×100)
ただし 信頼度は非対称 なので、どちらを前提にするかで解釈が変わることになります。
📘 シリーズ記事の流れ
次の記事 ▶️:

📚 シリーズトップ:




コメント